ABSTRACT
On any NASA contract, management is concerned about safety risks. This paper discusses a recommended improvement in the current method of communicating the level of these risks to management by the safety community.
One of the many developments which followed the Challenger accident of 1986 was a growing realization within the aerospace community that there was a basic communication difficulty between the safety professionals, engineers who were familiar with the problems encountered in hardware use, and the managers who were responsible for the use of that hardware. Safety and management were talking to each other, but it was not certain that each fully understood what the other was saying. In an effort to improve communication of hazards to management, NASA established the NSTS Hazard Prioritization Working Group in March of 1987. The working group published what was essentially a description of the problem and recommendations for priority of effort for its solution. The purpose of the working group was to develop a hazard prioritization technique that would improve the manner in which risks are worked and brought to higher management attention.
Many major element contractors began studying this challenges presented by the concept of hazard prioritization. As studies progressed, many considerations were examined to provide a more efficient and effective method of communicating hazard information. The final product was incorporation of the conclusions of the Hazard Prioritization Working Group into NSTS 22254, Methodology for Conduct of Space Shuttle Program Hazard Analyses. The current version, Revision A, dated April 30, 1991 describes a "Risk Matrix" which shows graphically twelve different combinations of likelihood and severity levels which, taken together, define levels of risk. Only one of these levels is considered an unacceptable risk, while four of them define "controlled" hazards.
Many of these considerations appear to be applicable to a more precise method of evaluating hardware defects or discrepancies in a manner which can be used by management to establish a priority for consideration and resolution effort. This paper is an attempt to apply some of these considerations to this task.
First of all, it may be helpful to evaluate hardware discrepancies in terms of their effect on the overall mission. The following might be reasonably effective discriminators in a determination of the risk created by the discrepancy under consideration:
a. The discrepant part is not a part of the flight vehicle or mission critical hardware, and cannot reasonably be expected to impact the mission.Another consideration which may be of value in an evaluation of a defect or discrepancy is the degree to which the discrepancy is likely to be discovered. A number of possibilities suggest themselves.b. The discrepant part is installed on the flight vehicle or mission critical hardware, but is not likely to affect safety of the spacecraft or crew, or the accomplishment of the mission.
c. The uncorrected discrepancy is likely to cause failure of a backup system, which could be expected to require minor contingency effort without noticeable impact to the mission if the primary system failed.
d. The uncorrected discrepancy is likely to cause failure of a backup system, which could be expected to require implementation of a contingency plan without significant impact to the mission if the primary system failed.
e. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to require implementation of a contingency plan which would not necessarily interrupt the mission.
f. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to result in environmental damage or to require implementation of a contingency plan which would interrupt, but not necessarily curtail, the mission.
g. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to result in environmental damage or to require unplanned contingency action which would interrupt, but not necessarily curtail, the mission.
h. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to result in environmental damage or to require an orderly process of mission curtailment, but not necessarily immediate emergency action or the loss of the spacecraft, crew or ground facilities.
i. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to result in environmental damage or to require an orderly process of mission termination, but not necessarily in the loss of the spacecraft, crew or ground facilities.
j. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to result in environmental damage or to require emergency action which would likely result in immediate mission termination, but not necessarily in the loss of the spacecraft, crew or ground facilities.
k. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to cause the loss of the spacecraft, crew or major ground facilities or major ground equipment, or environmental catastrophe, unless emergency measures, which would likely result in mission termination, were initiated in an orderly manner after discussion with ground control.
l. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to cause the loss of the spacecraft, crew or major ground facilities or major ground equipment, or environmental catastrophe, unless emergency measures, which would be likely to result in mission termination, were promptly initiated.
m. The uncorrected discrepancy is likely to cause failure of a backup system, which, upon failure of the primary system, could be expected to cause the loss of the spacecraft, crew or major ground facilities or major ground equipment or environmental catastrophe, unless emergency measures, which would require mission termination, were promptly initiated.
n. The uncorrected discrepancy is likely to cause failure of a backup system, which could be expected to cause the loss of the spacecraft, crew or major ground facilities, or an environmental catastrophe, with no possibility of recovery if the primary system failed.
o. The uncorrected discrepancy alone could be expected to require minor contingency effort without noticeable impact to the mission.
p. The uncorrected discrepancy alone could be expected to require implementation of a contingency plan without significant impact to the mission.
q. The uncorrected discrepancy alone could be expected to require implementation of a contingency plan which would not necessarily interrupt the mission.
r. The uncorrected discrepancy alone could be expected to result in environmental damage or to require implementation of a contingency plan which would interrupt, but not necessarily curtail, the mission.
s. The uncorrected discrepancy alone could be expected to result in environmental damage or to require unplanned contingency action which would interrupt, but not necessarily curtail, the mission.
t. The uncorrected discrepancy alone could be expected to result in environmental damage or to require an orderly process of mission curtailment, but not necessarily immediate emergency action or the loss of the spacecraft, crew or ground facilities.
u. The uncorrected discrepancy alone could be expected to result in environmental damage or to require an orderly process of mission termination, but not necessarily in the loss of the spacecraft, crew or ground facilities.
v. The uncorrected discrepancy alone could be expected to result in environmental damage or require emergency action which would likely result in immediate mission termination, but not necessarily in the loss of the spacecraft, crew or ground facilities.
w. The uncorrected discrepancy alone could be expected to cause the loss of the spacecraft, crew or major ground facilities or major ground equipment, or an environmental catastrophe, unless emergency measures, which would likely result in mission termination, were initiated in an orderly manner after discussion with ground control.
x. The uncorrected discrepancy alone could be expected to cause the loss of the spacecraft, crew or major ground facilities or major ground equipment, or an environmental catastrophe, unless emergency measures, which would be likely to result in mission termination, were promptly initiated.
y. The uncorrected discrepancy alone could be expected to cause the loss of the spacecraft, crew or major ground facilities or major ground equipment, or an environmental catastrophe, unless emergency measures, which is likely to require mission termination, were promptly initiated.
z. The uncorrected discrepancy alone could be expected to cause the loss of the spacecraft, crew or major ground facilities, or an environmental catastrophe, with no possibility of recovery.
a. The discrepancy is immediately obvious from a cursory examination of the packaged part.The foregoing considerations are similar in that they define an ascending order of risk. The first group constitutes an ordering of risks to the spacecraft, crew, mission and environment, while the second group constitutes an ordering of risks that the discrepancy will not be discovered. Management would be concerned with a third category of risk, that of impact to the program and, ultimately to the viability of the corporation. This consideration suggests a third set of evaluation criteria.b. The discrepancy is likely to be detected by receiving inspection.
c. The discrepancy is immediately obvious by visual inspection, but cannot be detected during receiving inspection due to packaging or some other characteristic which conceals the defect until the discrepant part is ready to be used.
d. The discrepancy cannot be discovered by receiving inspection, but is of such a nature that the discrepant part cannot be incorporated into the flight vehicle (due to improper fit, mismatched mating surfaces, or the like).
e. The discrepancy cannot be discovered by receiving inspection, but is of such a nature that it would be obvious during or prior to an attempt to incorporate the discrepant part into the flight vehicle.
f. The discrepancy cannot be discovered by receiving inspection, but is likely to be noted prior to an attempt to incorporate the discrepant part into the flight vehicle.
g. The discrepancy can be discovered only during incorporation into the flight vehicle.
h. The discrepancy can be discovered only after it is incorporated into the flight vehicle.
i. The discrepancy can be discovered only during or after final assembly.
j. The discrepancy can be discovered only after spacecraft assembly (orbiter mate in the case of the Space Shuttle).
k. The discrepancy can be discovered only after rollout.
l. The discrepancy can be discovered only during countdown to launch.
m. The discrepancy can be discovered only after commitment to launch.
n. The discrepancy can be discovered only by its effect on flight performance.
o. The discrepancy cannot be discovered in time to avert its undesired effects.
a. The discrepancy represents a potential for minor rework, for which the corporation is contractually liable, but which is not likely to impact delivery or other major production milestones.Historically, ranking of hazards has employed a two dimensional graphical method in which the perceived severity of the hazard is represented on one axis and the assumed likelihood of occurrence is represented on the other. This method is used by both NASA and the Department of Defense with varying degrees of success, which suggests that ranking of discrepancy importance or criticality could be accomplished by much the same method. However, while a graphical method presents the assessment of risk in a method which can be readily visualized, the methods traditionally employed have suffered from an effort to create arbitrary boundaries between varying degrees of risk. Thus a "1A hazard" is considered to be of more concern than a "2B hazard," but what the precise distinction between them is, either in terms of severity or likelihood of occurrence, has often been left to a rather subjective judgement. For this reason, it might be more helpful to avoid arbitrary categories of risk altogether in a determination of the importance or criticality of discrepancies, in favor of a purely numerical approach.b. The discrepancy represents a potential for minor production delay, resulting in delay in achievement of one or more production milestones, but which can be remedied prior to delivery, which should not be adversely impacted, and for which the contractor would not be contractually liable.
c. The discrepancy represents a potential for significant production delay, resulting in delay in achievement of one or more major milestones, but not necessarily a delay in delivery, or of major rework of one or more assemblies, but for which the corporation would not be contractually liable.
d. The discrepancy represents a potential for significant production delay, resulting in significant delay in delivery or rejection of assemblies of high dollar value, for which the corporation would not be contractually liable.
e. The discrepancy represents a potential for major production delay, resulting in major delay in delivery or rejection of major subassemblies, for which the corporation would not be contractually liable.
f. The discrepancy represents a potential for rearrangement of the flight schedule, not involving significant postponement of flight, for which the corporation would not be contractually liable.
g. The discrepancy represents a potential for minor production delay, resulting in delay in achievement of one or more contractual milestones, but which can be remedied prior to delivery, which should not be adversely impacted.
h. The discrepancy represents a potential for postponement of flights for a relatively short period of time, but for which the corporation would not be contractually liable.
i. The discrepancy represents a potential for significant production delay, resulting in delay in achievement of one or more major milestones, but not necessarily a delay in delivery, or of major rework of one or more assemblies, for which the corporation would be contractually liable.
j. The discrepancy represents a potential for postponement of further missions for a protracted period, but for which the corporation would not be contractually liable.
k. The discrepancy represents a potential for significant production delay, resulting in significant delay in delivery or rejection of assemblies of high dollar value, for which the corporation would be contractually liable.
l. The discrepancy represents a potential for major impact to the Space Shuttle program involving postponement of further missions for an indefinite period, but for which the corporation would not be liable.
m. The discrepancy represents a potential for major production delay, resulting in major delay in delivery or rejection of major subassemblies, for which the corporation would be contractually liable.
n. The discrepancy represents a potential for rearrangement of the flight schedule, not involving significant postponement of flight, for which the corporation would be held pecuniarily liable.
o. The discrepancy represents a potential for postponement of flights for a relatively short period of time, for which the corporation would be held pecuniarily liable.
p. The discrepancy represents a potential for postponement of further missions for a protracted period, for which the corporation would be held pecuniarily liable.
q. The discrepancy represents a potential for major impact to the Space Shuttle program involving postponement of further missions for an indefinite period, for which the corporation would be pecuniarily, and possibly criminally, liable.
The listing of the three foregoing parameters suggests that there are three areas of concern which might properly be evaluated as separate numerical quantities. This can be done by making the numerical representation of discrepancy criticality a vector. The degree of concern or attention given to resolution of the discrepancy could then be represented by a definition of the absolute length of the vector.
This leaves open the problem of how to assign scalar values to each of the parameters which have been listed. Many methods could be devised, but one method which may be generally applied is a graph of the form:
Y is the value assigned to each parameter,
A is the maximum value to be assigned the greatest parameter,
X is the order of each parameter within the group,
B is the number of parameters within the group, and
n is a value chosen to skew the calculated relationship between X and Y.
This relationship is shown in the graph on the following page. Assume, for example, a group of 26 parameters, such as the listed effects on the overall mission. When arranged this way, B is 26, and the order in which each effect appears is X. If a value of 100 is chosen as the maximum value of this parameter, A will be equal to 100.
The value of n may be chosen arbitrarily. A value less than 1 will skew the value of the parameter Y to the left. In other words, The value of Y will tend to be large for even small values of X, providing greater intervals between values of Y for low values of X. A value of n greater than 1 will have the opposite effect, that of discriminating better between high values of X. If n is given a value of one, the relationship between X and Y is linear.
The use of this method may be shown by the following example:
a. For the purposes of discussion, we will assume that the maximum value assigned to a parameter chosen to represent potential consequences of a hardware discrepancy is to be 100, and that we would like this parameter to rise fairly rapidly for large values of X, which requires n to be somewhat greater than unity. Choosing n1 to be 1.2, potential consequences of the uncorrected discrepancy are assigned the following values. Note that a value of 50 for Y corresponds to an effect which is greater than failure of a backup system (which would not be of concern in the absence of other failures), and failure of a primary system requiring minor contingency effort without noticeable impact on the mission. This might represent a minimum level of "higher management concern," so a value midway between zero and 100 works out nicely. Assigning n1 to be 1.2 provides the following values for Y:It should be noted that if one of the parameters is not zero and the other two are zero (the discrepant part can be used as is with no impact on the mission, but cannot be discovered until some time in the build cycle, for example), the vector length is simply the value of the non-zero parameter (for any p whatever). In particular, if any one of the parameters is 50, our threshold of higher management concern, then the vector length will be at least 50, which preserves the "management alert" feature of attracting management attention if even only one of the parameters is 50 or above.
(1) Not a part of the flight vehicle or mission critical hardware, and cannot reasonably be expect to impact the mission - 2.00
(2) Installed on the flight vehicle or mission critical hardware, but not likely to affect safety of the spacecraft or crew, or the accomplishment of the mission - 4.61
(3) Failure of a backup system, requiring minor contingency effort without noticeable impact to the mission if the primary system failed - 7.49
(4) Failure of a backup system, requiring implementation of a contingency plan without significant impact to the mission if the primary system failed -10.58
(5) Failure of a backup system, requiring implementation of a contingency plan which could possibly interrupt the mission if the primary system failed - 13.83
(6) Failure of a backup system, requiring implementation of a contingency plan which would interrupt the mission if the primary system failed - 17.21
(7) Failure of a backup system, requiring unplanned contingency action which would interrupt the mission if the primary system failed - 20.71
(8) Failure of a backup system, requiring an orderly process of mission curtailment, but not necessarily immediate emergency action if the primary system failed - 24.31
(9) Failure of a backup system, requiring an orderly process of mission termination if the primary system failed - 28.0
(10) Failure of a backup system, requiring emergency action which would likely result in immediate mission termination if the primary system failed - 31.77
(11) Failure of a backup system, loss of the spacecraft, crew or major ground facilities or major ground equipment, or environmental catastrophe, unless emergency measures, with probable mission termination, were initiated in an orderly manner after discussion with ground control if the primary system failed - 35.62
(12) Failure of a backup system, loss of the spacecraft, crew or major ground facilities or major ground equipment, or environmental catastrophe, unless emergency measures, which would be likely to result in mission termination, were promptly initiated if the primary system failed - 39.54
(13) Failure of a backup system, loss of the spacecraft, crew or major ground facilities or major ground equipment or environmental catastrophe, unless emergency measures, which would require mission termination, were promptly initiated if the primary system failed - 43.53
(14) Failure of a backup system, loss of the spacecraft, crew or major ground facilities, or an environmental catastrophe, with no possibility of recovery if the primary system failed - 47.58
(15) Minor contingency effort without noticeable mission impact - 51.68
(16) Implementation of a contingency plan without significant impact to the mission - 55.84
(17) Implementation of a contingency plan but not necessarily interruption of the mission - 60.06
(18) Implementation of a contingency plan which would interrupt the mission - 64.32
(19) Unplanned contingency action and mission interruption - 68.63
(20) Orderly mission curtailment, short of emergency action - 72.99
(21) Orderly mission termination, but not likely loss of the spacecraft, crew or ground facilities - 77.39
(22) Immediate mission termination, but not likely loss of the spacecraft, crew or ground facilities - 81.84
(23) Orderly implementation of emergency measures with likely mission termination - 86.32
(24) Requires prompt emergency measures, which would be likely to result in mission termination - 90.84
(25) Requires prompt emergency measures, which would require mission termination - 95.40
(26) Loss of the spacecraft, crew or major ground facilities, or an environmental catastrophe, with no possibility of recovery - 100
b. We may consider the capability to discover the discrepancy in time to avert the aforementioned effects in two ways. First of all, the most serious concern would be associated with not being able to detect the discrepancy in time to avert its undesired effects. We might assign a maximum value of 100 to this parameter, A2, since the effects could be as serious as the foregoing worst case, which is loss of the spacecraft and crew. However, the "50% breakover point," or the minimum level of higher management concern (Y = 50), might be a defect which cannot be detected until final assembly (X = 9). Since B2 is 15 in this case, we can solve for n:
n2 = (log Y - log A2) / (log X - log B2) = 1.36 (approximately) .Use of the exact value of n = 1.3569154 provides the following values for Y:
(1) Immediately obvious from a cursory examination - 2.54
(2) Likely to be detected by receiving inspection - 6.50
(3) Immediately obvious by visual inspection, but cannot be detected during receiving inspection - 11.26
(4) Cannot be discovered by receiving inspection, but cannot be incorporated into the flight vehicle - 16.64
(5) Cannot be discovered by receiving inspection, but would be obvious prior to an attempt to incorporate into the flight vehicle - 22.52
(6) Cannot be discovered by receiving inspection, but likely to be noted prior to an attempt to incorporate into the flight vehicle - 28.84
(7) Can be discovered only during flight vehicle incorporation - 35.55
(8) Can be discovered only after flight vehicle incorporation - 42.61
(9) Can be discovered only during or after final assembly - 50.00
(10) Can be discovered only after spacecraft assembly - 57.68
(11) Can be discovered only after rollout - 65.65
(12) Can be discovered only during countdown to launch - 73.88
(13) Can be discovered only after commitment to launch - 82.35
(14) Can be discovered only by its effect on flight performance - 91.06
(15) Cannot be discovered in time to avert its undesired effects - 100
c. The values assigned to program impact or corporate liability can be determined from two considerations. The first is a determination of what degree of risk from either the potential effects of the discrepancy or its likelihood of being detected can be considered to be numerically equivalent to the maximum program risk, A3. This is ultimately a management decision, based upon judgement and the perception by management of several factors. Without going into a prolonged discussion of these factors, we may assume for the sake of example that the worst case program risk, that of postponement of further missions for an indefinite period, along with possible corporate pecuniary liability, might be roughly equivalent to loss of the spacecraft, crew or major ground facilities or major ground equipment, or an environmental catastrophe, unless emergency measures were promptly initiated. The latter risk has already been assigned a numerical value of 90.84. We may also consider that this risk would be equivalent to a defect which can be discovered only by its effect on flight performance, which has been given a value of 91.06. It would appear, then, that a maximum value, A3, of 91 might be appropriate for the risk to the program.
d. To maintain a lower limit of major concern of 50, we must determine what program risk is represented by this limit. For the purposes of discussion, we may assume that corporate liability for significant production delay, involving missing of major production milestones, represents this limit. This is the 9th parameter, so in this case, Y is 50 for an X of 9, and B3 is 17 for A1 = 91. Substituting these values into the equation:
n3 = (log Y - log A3) / (log X - log B3) we get
n3 = (log 50 - log 91) / (log 9 - log 17) = 0.94 (approximately) .The exact value of n = 0.9415835 provides the following numerical values for Y:
(1) Minor rework, corporation liable, which is not likely to impact delivery or other major production milestones - 6.32
(2) Minor production delay, delay in achievement of one or more production milestones which can be remedied prior to delivery, which should not be adversely impacted, corporation not liable - 12.13
(3) Significant production delay, delay in achievement of one or more major milestones, but not necessarily a delay in delivery, or of major rework of one or more assemblies, corporation not liable - 17.77
(4) Significant production delay, significant delay in delivery or rejection of assemblies of high dollar value, corporation not liable - 23.30
(5) Major production delay, major delay in delivery or rejection of major subassemblies, corporation not liable - 28.75
(6) Rearrangement of the flight schedule, not involving significant postponement of flight, corporation not liable - 34.13
(7) Minor production delay, delay in achievement of one or more contractual milestones which can be remedied prior to delivery, which should not be adversely impacted, corporation liable - 39.46
(8) Postponement of flights for a short time, corporation not liable - 44.75
(9) Significant production delay, delay in achievement of one or more major milestones, but not necessarily a delay in delivery, or of major rework of one or more assemblies, corporation liable - 50.00
(10) Postponement of further missions for a protracted period, corporation not liable - 55.21
(11) Significant production delay, delay in delivery, rejection of assemblies of high dollar value, corporation liable - 60.40
(12) Major impact to the Space Shuttle program, postponement of further missions for an indefinite period, corporation not liable - 65.56
(13) Potential for major production delay, major delay in delivery or rejection of major subassemblies, corporation liable - 70.69
(14) Rearrangement of the flight schedule, no significant postponement of flight, corporation liable - 75.80
(15) Postponement of flights for a short time, corporation liable - 80.88
(16) Postponement of further missions for a protracted period, corporation liable - 85.95
(17) Major impact to the Space Shuttle program, postponement of further missions for an indefinite period, corporation liable, possible criminal penalty - 91.00
e. The only remaining requirement is to define the vector length. In euclidean geometry, a vector L is represented as:
L = [a b c] where a, b and c are scalar quantities. The length of the vector L is defined as:
|L| = (ap + bp + cp)(1/p) where p = 2 and a, b and c are the lengths of the vector projected along the x, y and z axes, respectively. However, there is nothing in this example which constrains our model to follow euclidean geometry, so we are free to choose p arbitrarily, noting that p will be uniquely defined by a single non-trivial equation. If p equals 1, the length of the vector is simply the sum of its individual scalar components. We may desire that L have some maximum length, say 100, for the most critical situation in which all the parameters Y are maximum, that is, when Y1 = A1, Y2 = A2 and Y3 = A3. However, it should be noted that L can never be be shorter than its greatest component for positive values of p, nor longer than its least component for negative values of p. We are free, however, to choose maximum vector lengths L larger than the greatest component or shorter than the least component, respectively. One possible value for maximum L is 150, which gives us a range of 100 for those values above the threshold of "higher management concern." Subtracting 50 from the vector length would thus provide a scale from 0 to 100 for convenient ranking of management attention priority. Since A1, A2 and A3 are 100, 100 and 91, respectively, we have the equation:
|L|p = 150p = ap + bp + cp = 100p + 100p + 91p. In this case, p works out to about 2.5286. Therefore, for any a, b and c,
|L| = (a2.5286 + b2.5286 + c2.5286)0.3955.
To illustrate the use of this concept to evaluate discrepancies to establish a priority for consideration and resolution effort, assume that we are concerned with a discrepancy which could cause failure of a backup system in a space vehicle. Further, suppose that failure of the primary system, could be expected to result in environmental damage or to require implementation of a contingency plan which would interrupt, but not necessarily curtail, the mission. We further assume that the discrepancy cannot be discovered by receiving inspection, but is likely to be noted prior to an attempt to incorporate the discrepant part into the flight vehicle, and that because of this the discrepancy represents a potential for minor production delay, while the discrepant part is replaced at the scheduled time of installation in the vehicle. This could result in delay in achievement of one or more contractual milestones, but the time lost could probably be remedied prior to delivery, so final delivery should not be adversely impacted.
First of all, we note that the value a assigned to failure of a backup system, requiring implementation of a contingency plan which would interrupt the mission if the primary system failed is 17.21. If the discrepancy cannot be discovered by receiving inspection, but is likely to be noted prior to an attempt to incorporate the part into the flight vehicle, a value of 28.84 is assigned to b. Minor production delay, delay in achievement of one or more contractual milestones which can be remedied prior to delivery, and which should not adversely impact delivery, is assigned a value c of 39.46. Substituting these values into the equationOn the other hand, consider a part, possibly furnished by the Government, the failure of which could cause failure of a backup system. In this example, failure of the primary system could be expected to result in environmental damage or to require an orderly process of mission curtailment, but not necessarily immediate emergency action or the loss of the spacecraft, crew or ground facilities. Furthermore, with GFP, it is likely that the discrepancy could be discovered only after it is incorporated into the flight vehicle. Such a discrepancy would likely result in postponement of flights for a relatively short period of time while existing flight vehicles were checked for the discrepancy. In this case, assume that the corporation would not be contractually liable for the delay. The values assigned to this situation are as follows:
|L| = (a2.5286 + b2.5286 + c2.5286)0.3955
yields
|L| = (17.212.5286 + 28.842.5286 + 39.462.5286)0.3955 = 47.22 Therefore, although this problem would no doubt require resolution, it is not one which would warrant higher management concern.
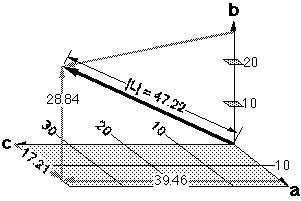
L = [17.21 28.84 39.46]
a. Failure of a backup system, requiring an orderly process of mission curtailment, but not necessarily immediate emergency action if the primary system failed - 24.31While the foregoing discussion shows the logic involved in the determination of the vector lengths which indicate the degree of management concern, it is not necessary to go through the logic process in order to compute the values. The order of the parameters may be taken from a list and simply "plugged into" an equation to determine |L|. In the above examples,b. Can be discovered only after it is incorporated into the flight vehicle - 42.61
c. Postponement of flights for a short time, corporation not liable - 44.75
|L| = (24.3125286 + 42.6125286 + 44.7525286)0.3955 = 59.98. In this case, the discrepancy would warrant higher management attention even though the individual parameters were below the management alert threshold.
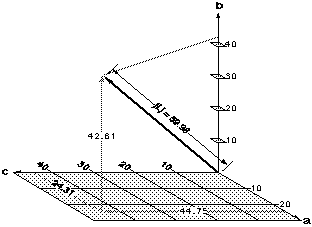
L = [24.31 42.61 44.75]
If the corporation were found liable for the delay, c would become 80.88, which itself would be enough to attract higher management attention. In addition, computation of the vector length yields:
|L| = (24.3125286 + 42.6125286 + 80.8825286)0.3955 = 88.22,
which is definitely an indicator of management concern.
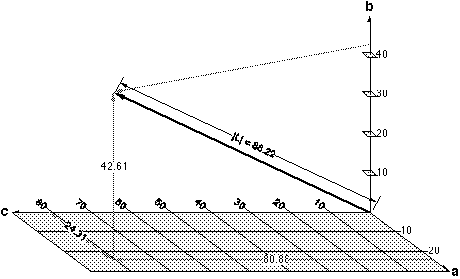
L = [24.31 42.61 80.88]
Since only X1, X2 and X3 are variables in this equation, it can be simplified to:
which is equal to 47.46 for the first condition, 60.28 for the second and 88.74 for the third (corporation liable) situation. These values are within 1/2 of one percent of the values computed previously, so the simplified equations shown above are precise enough for the purpose intended.
The instructions for computation of |L| therefore resolve to the following steps:
a. Select the order of the first parameter. This will be a number from 1 to 26It should be noted that this method of hazard prioritization permits tailoring to suit the needs of the program to which it is applied. The selection of n1, n2, n3, A3 and p are arbitrary, as are the description and ordering of parameters, and can be changed as necessary to provide the degree of management visibility and involvement desired.b. Raise that number to the power of 3.034
c. Multiply the result by 5.8.
d. Select the order of the second parameter, a number from 1 to 15.
e. Raise that number to the power of 3.431.
f. Multiply the result by 10.5.
g. Select the order of the third parameter, a number from 1 to 17.
h. Raise that number to the power of 2.381.
i. Multiply the result by 105.7.
j. Add the products arrived at in c, f and i, above, and raise the sum to the power of 0.396.
k. The result is |L|, which will be between zero and 150. Anything over 100 is reportable as a higher management concern.
Prioritizing hazards in this way allows a more rigorous defintion and comparison of risk, and can be used in hazard reports, safety analysis reports, and similar documents which are submitted by the element contractors to NASA for review. It also provides a more rigorous method for analyzing the effectiveness of the safety effort to mitigate risks which have been reduced through the hazard reduction precedence sequence described in NHB 5300.4 (1D-2).
At levels below NASA Headquarters, this method allows progressively higher levels of management to confine their attention to hazards rigorously identified by a precise degree of concern rather than simply selecting the "top ten" from some particular list. For example, the contractor top management might be concerned with all hazards with L over 50, Level III with L over 60, Level II with L over 70, Level I with L over 80, NASA Headquarters with L over 90, and so on. Since the maximum value of L is 150, this leaves a rather large range of level of concern at NASA Headquarters, but the actual number of hazards requiring this level of concern would be expected to be small. Concerns with L over 90 would involve hazards of a severity equal to those which, in the absence of other exacerbating factors, would require prompt emergency measures likely to result in mission termination, those which could be discovered only by their effect on flight performance, or those which would have a major impact to the Space Shuttle program with postponement of further missions for an indefinite period and possible civil and criminal prosecution.
The methods outlined in this paper represent a powerful means of arranging concerns in a hierarchy which permits assignment of priority for resolution effort, and quickly and precisely to communicate the level of risk to all levels of management. They can be tailored to individual situations by proper choices of p and of A, B, and n for each of the parameter categories. There is nothing in these methods which limits them to consideration of only three categories, which therefore makes them useful when many different aspects of a particular concern must be taken into consideration. Although these methods look complicated, very simple computer programs, easily within the capability of pocket programmable calculators, can be written to allow them to be used quickly and efficiently by untrained individuals. Their use can be of significant value for the efficient and effective communication of levels of risk to management, and for the assignment of resources for resolution of complex quality control and safety problems.